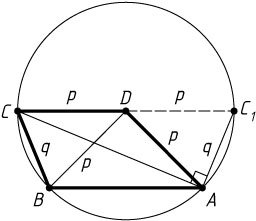
145. Основание CD
, диагональ BD
и боковая сторона AD
трапеции ABCD
равны p
. Боковая сторона BC
равна q
. Найдите диагональ AC
.
Ответ. \sqrt{4p^{2}-q^{2}}
.
Указание. Проведите окружность с центром в точке D
и радиусом p
.
Решение. Окружность с центром в точке D
и радиусом p
проходит через точки A
, B
и C
. Если CC_{1}
— диаметр окружности, то ABCC_{1}
— равнобедренная трапеция, AC_{1}=BC=q
.
Поскольку \angle CAC_{1}=90^{\circ}
(точка A
лежит на окружности с диаметром CC_{1}
), то
AC^{2}=CC^{2}_{1}-AC^{2}_{1}=4p^{2}-q^{2}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1977, № 4, вариант 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 59
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 101
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 38, с. 142
