146. На сторонах AB
, BC
и AC
треугольника ABC
взяты соответственно точки D
, E
и F
так, что DE=BE
, FE=CE
. Докажите, что центр описанной около треугольника ADF
окружности лежит на биссектрисе угла DEF
.
Указание. Пусть O
— центр описанной окружности треугольника ADF
. Докажите, что точки E
, F
, O
и D
лежат на одной окружности.
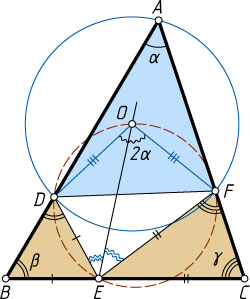
Решение. Пусть O
— центр описанной окружности треугольника ADF
. Обозначим углы треугольника ABC
через \alpha
, \beta
, \gamma
соответственно. Тогда
\angle FED=180^{\circ}-(180^{\circ}-2\beta)-(180^{\circ}-2\gamma)=
=2(\beta+\gamma)-180^{\circ}=180^{\circ}-2\alpha\gt0.
Поэтому \alpha
— острый угол, \angle DOF=2\angle DAF=2\alpha
, значит, точки E
, F
, O
, D
лежат на одной окружности. Вписанные в эту окружность углы OED
и OEF
равны, так как они опираются на равные хорды OD
и OE
— радиусы описанной окружности треугольника ADF
. Следовательно, EO
— биссектриса угла DEF
.
Источник: Всесоюзная олимпиада по математике. — 1989, XXIII
