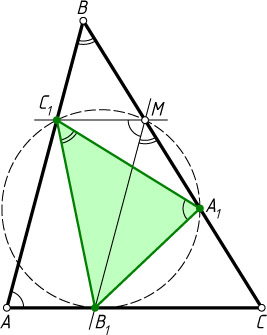
147. На сторонах AB
, BC
и CA
треугольника ABC
зелёной краской отметили соответственно точки C_{1}
, A_{1}
и B_{1}
, отличные от вершин треугольника. Оказалось, что \frac{AC_{1}}{C_{1}B}=\frac{BA_{1}}{A_{1}C}=\frac{CB_{1}}{B_{1}A}
, а \angle BAC=\angle B_{1}A_{1}C_{1}
. Докажите, что треугольник с зелёными вершинами подобен треугольнику ABC
.
Указание. На стороне BC
возьмите такую точку M
, для которой C_{1}M\parallel AC
. Тогда около четырёхугольника MC_{1}B_{1}A_{1}
можно описать окружность.
Решение. Пусть M
— такая точка на стороне BC
, для которой C_{1}M\parallel AC
. Предположим, что M
между C
и A_{1}
. Тогда
\frac{CM}{MB}=\frac{AC_{1}}{C_{1}B}=\frac{CB_{1}}{B_{1}A}.
Поэтому MB_{1}\parallel AB
. Тогда
\angle B_{1}MC_{1}=\angle BAC=\angle B_{1}A_{1}C_{1}.
Поскольку отрезок B_{1}C_{1}
виден из точек M
и A_{1}
под одним и тем же углом, то точки C_{1}
, M
, A_{1}
и B_{1}
лежат на одной окружности. Следовательно,
\angle A_{1}B_{1}C_{1}=\angle A_{1}MC_{1}=\angle C,
и треугольники ABC
и A_{1}C_{1}B_{1}
подобны по двум углам.
Аналогично для случая, когда M
между B
и A_{1}
.
Если же M
совпадает с A_{1}
, утверждение очевидно.
Автор: Шарыгин И. Ф.
Источник: Журнал «Квант». — 1989, № 11, с. 67, задача 6
