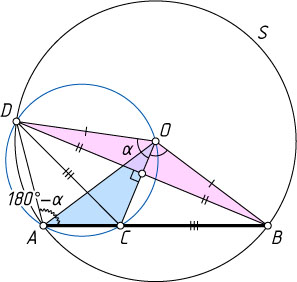
148. На хорде AB
окружности S
с центром в точке O
взята точка C
. D
— вторая точка пересечения окружности S
с окружностью, описанной около треугольника ACO
. Докажите, что CD=CB
.
Указание. OC
— биссектриса угла DOB
.
Решение. Рассмотрим случай, когда точки D
и C
лежат по разные стороны от AO
. Пусть \angle DOC=\alpha
. Тогда
\angle DAC=180^{\circ}-\alpha,~\angle DOB=360^{\circ}-2\angle DAB=
=360^{\circ}-(360^{\circ}-2\alpha)=2\alpha.
Значит, OC
— биссектриса угла DOB
. Поскольку треугольник DOB
равнобедренный, то прямая OC
— серединный перпендикуляр к отрезку DB
. Следовательно, CD=CB
.
Автор: Колпаков С.
Источник: Московская математическая олимпиада. — 1980, XLIII, 8 класс
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 8, с. 142
Источник: Журнал «Квант». — 1980, № 3, с. 26, М611
Источник: Задачник «Кванта». — М611
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 702, с. 88
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.36, с. 35
