149. В треугольнике ABC
угол C
тупой. На стороне AB
отмечены точки E
и H
, на сторонах AC
и BC
— точки K
и M
соответственно. Оказалось, что AH=AC
, BE=BC
, AE=AK
, BH=BM
. Докажите, что точки E
, H
, K
, M
лежат на одной окружности.
Указание. Докажите, что CK=CM
.
Решение. Обозначим углы треугольника ABC
через \alpha
, \beta
, \gamma
соответственно. Поскольку
CK=CA-AK=AH-AE=EH=BE-BH=BC-BM=CM,
то
\angle CKM=90^{\circ}-\frac{\gamma}{2}.
Поэтому
\angle AKM=90^{\circ}+\frac{\gamma}{2}.
Поскольку
\angle AKE=90^{\circ}-\frac{\alpha}{2},
то
\angle EKM=180^{\circ}-\angle AKE-\angle CKM=180^{\circ}-\left(90^{\circ}-\frac{\alpha}{2}\right)-\left(90^{\circ}-\frac{\gamma}{2}\right)=
=\frac{\alpha}{2}+\frac{\gamma}{2}=90^{\circ}-\frac{\beta}{2}=\angle MHB=180^{\circ}-\angle MHE.
Следовательно, около четырёхугольника EKMH
можно описать окружность.
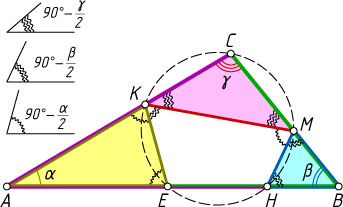
Примечание. Можно доказать, что на этой же окружности лежит и точка C
.
Источник: Московская математическая олимпиада. — 1972, XXXIV, 1-й тур, 9 класс
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 10, с. 121
