152. На плоскости даны прямая l
и две точки A
и B
по одну сторону от неё. На прямой l
выбраны точка M
, сумма расстояний от которой до точек A
и B
наименьшая, и точка N
, для которой расстояния от A
и B
равны: AN=BN
. Докажите, что точки A
, B
, M
, N
лежат на одной окружности.
Указание. Точка, симметричная точке B
относительно прямой l
, лежит на окружности с центром в точке N
и радиусом AN
.
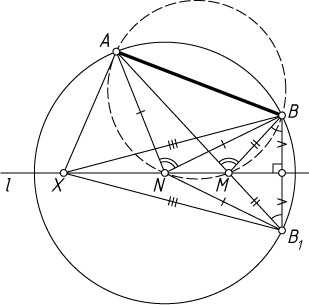
Решение. Пусть B_{1}
— точка, симметричная точке B
относительно прямой l
. Докажем, что точка M
, о которой говорится в условии задачи, — это точка точка пересечения AB_{1}
и l
. Действительно, если X
— произвольная точка прямой l
, отличная от M
, то
AX+BX=AX+B_{1}X\gt AB_{1}=AM+MB_{1}=AM+BM.
Из условия задачи также следует, что NA=NB=NB_{1}
, поэтому точки A
, B
и B_{1}
лежат на окружности с центром в точке N
радиуса AN
. Угол ANB
— центральный угол этой окружности, поэтому \angle ANB=2\angle AB_{1}B
. Угол AMB
— внешний угол равнобедренного треугольника BMB_{1}
. Поэтому
\angle AMB=2\angle AB_{1}B=\angle ANB.
Значит, отрезок AB
виден из точек M
и N
под одним и тем же углом. Следовательно, точки M
, N
, A
и B
расположены на одной окружности.
Автор: Курляндчик Л. Д.
Источник: Журнал «Квант». — 1987, № 7, с. 38, М1031
Источник: Задачник «Кванта». — М1031
