153. Докажите, что если в выпуклом пятиугольнике ABCDE
имеют место равенства \angle ABC=\angle ADE
и \angle AEC=\angle ADB
, то \angle BAC=\angle DAE
.
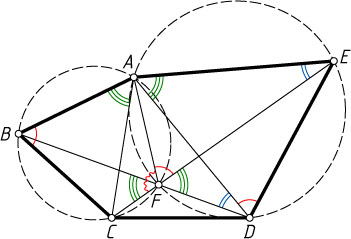
Указание. Пусть F
— точка пересечения диагоналей EC
и DB
. Докажите, что четырёхугольники AEDF
и AFCB
— вписанные.
Решение. Пусть F
— точка пересечения диагоналей EC
и DB
. Поскольку \angle AEC=\angle ADB
, то отрезок AF
виден из точек E
и D
под одним и тем же углом. Поэтому точки A
, E
, D
, F
лежат на одной окружности. Тогда
\angle AFE=\angle ADE=\angle ABC,~\angle AFC+\angle ABC=180^{\circ}.
Поэтому точки A
, B
, C
и F
также лежат на одной окружности. Следовательно,
\angle CAB=\angle CFB=\angle EFD=\angle EAD.
Автор: Сергеев И. Н.
Источник: Всесоюзная олимпиада по математике. — 1987, XXI
Источник: Журнал «Квант». — 1987, № 11, с. 51, задача 2
