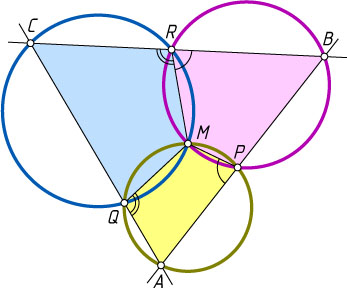
154. Три окружности имеют общую точку M
и попарно пересекаются в точках P
, Q
, R
. Через произвольную точку A
одной из окружностей, лежащую на дуге PQ
, не содержащей точки M
, и точки P
и Q
, в которых окружность пересекает две другие окружности, проведены прямые, пересекающие эти же две окружности в точках B
и C
. Докажите, что точки B
, C
и R
лежат на одной прямой.
Указание. Докажите, что \angle BRM+\angle CRM=180^{\circ}
.
Решение. Четырёхугольники BRMP
, APMQ
и CQMR
— вписанные. Поэтому
\angle BRM=180^{\circ}-\angle BPM=\angle APM,~\angle MRC=\angle AQM,
\angle APM+\angle AQM=180^{\circ}.
Следовательно,
\angle BRM+\angle CRM=180^{\circ}.
Поэтому точки B
, C
и R
лежат на одной прямой.
Источник: Всероссийская олимпиада школьников. — 1986-87, XIII, IV этап, 9 класс
Источник: Журнал «Квант». — 1987, № 10, с. 60, задача 3
