158. Через точку O
внутри выпуклого четырёхугольника ABCD
проведены четыре окружности одинакового радиуса, каждая из которых касается двух смежных сторон четырёхугольника. Докажите, что около четырёхугольника ABCD
можно описать окружность.
Указание. Четырёхугольник с вершинами в центрах окружностей — вписанный.
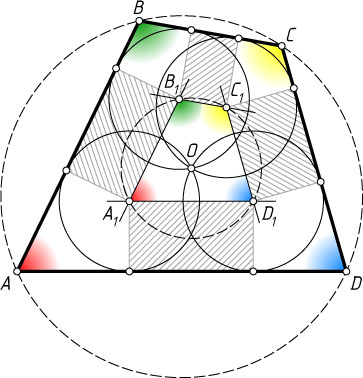
Решение. Пусть A_{1}
, B_{1}
, C_{1}
, D_{1}
— центры окружностей. Эти точки лежат на окружности с центром O
и радиусом OA_{1}
. Стороны четырёхугольника ABCD
соответственно параллельны сторонам внутреннего четырёхугольника A_{1}B_{1}C_{1}D_{1}
. Поэтому углы этих четырёхугольников соответственно равны.
Поскольку четырёхугольник A_{1}B_{1}C_{1}D_{1}
— вписанный, то сумма его противоположных углов равна 180^{\circ}
. Тогда сумма противоположных углов четырёхугольника ABCD
также равна 180^{\circ}
. Следовательно, он вписанный.
Источник: Всероссийская олимпиада школьников. — 1986, XII, 8 класс
Источник: Журнал «Квант». — 1986, № 10, с. 53, задача 1, 8 класс
Источник: Олимпиада «Высшая проба» (математическая олимпиада ВШЭ). — 2016, заключительный этап, задача 5, 10 класс
