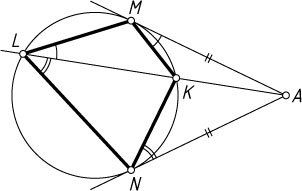
159. Из точки A
, расположенной вне окружности, проведены к ней две касательные AM
и AN
(M
и N
— точки касания) и секущая, пересекающая окружность в точках K
и L
. Докажите, что \frac{LM}{MK}=\frac{LN}{NK}
.
Решение. Из теоремы об угле между касательной и хордой следует, что
\angle AMK=\angle KLM=\angle ALM,
поэтому треугольник AMK
подобен треугольнику ALM
, значит, \frac{LM}{MK}=\frac{AL}{AM}
. Аналогично \frac{LN}{NK}=\frac{AL}{AN}
, а так как AN=AM
(как отрезки касательных, проведённых к окружности из одной точки), то \frac{LM}{MK}=\frac{LN}{NK}
.
Что и требовалось доказать.