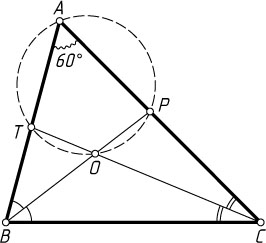
161. В треугольнике ABC
биссектрисы BP
и CT
пересекаются в точке O
. Известно, что точки A
, P
, O
и T
лежат на одной окружности. Найдите угол A
.
Ответ. 60^{\circ}
.
Указание. \angle TOP=90^{\circ}+\frac{1}{2}\angle A
.
Решение. Заметим, что
\angle POT=\angle BOC=180^{\circ}-\frac{1}{2}(\angle B+\angle C)=180^{\circ}-\frac{1}{2}(180^{\circ}-\angle A)=90^{\circ}+\frac{1}{2}\angle A.
Поскольку четырёхугольник APOT
вписанный, то
\angle A+\angle POT=180^{\circ}.
Следовательно,
\angle A+90^{\circ}+\frac{1}{2}\angle A=180^{\circ}.
Отсюда находим, что \angle A=60^{\circ}
.
Источник: Журнал «Квант». — 1984, № 10, с. 55, задача 15
