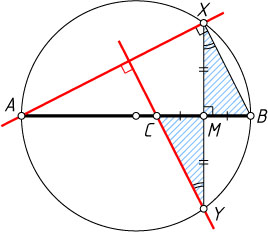
164. Дана окружность, её диаметр AB
и точка C
на этом диаметре. Постройте на окружности две точки X
и Y
, симметричные относительно диаметра AB
, для которых прямая YC
перпендикулярна прямой XA
.
Указание. Докажите, что XB\parallel YC
.
Решение. Предположим, что искомые точки X
и Y
построены. Тогда \angle AXB=90^{\circ}
. Поэтому XB\parallel YC
.
Пусть M
— точка пересечения отрезка XY
с диаметром AB
. Прямоугольные треугольники XMB
и YMC
равны (по катету и острому углу). Следовательно, CM=MB
, т. е. M
— середина отрезка BC
.
Отсюда вытекает следующее построение. Через середину M
отрезка BC
проводим прямую, перпендикулярную данному диаметру AB
. Эта прямая пересекает окружность в искомых точках X
и Y
.
Источник: Всесоюзная олимпиада по математике. — 1970, IV, 8 класс
Источник: Журнал «Квант». — 1970, № 9, с. 49, М41
Источник: Задачник «Кванта». — М41
Источник: Васильев Н. Б., Егоров А. А. Задачи всесоюзных математических олимпиад. — М.: Наука, 1988. — с. 41, № 129
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 8.71, с. 202
