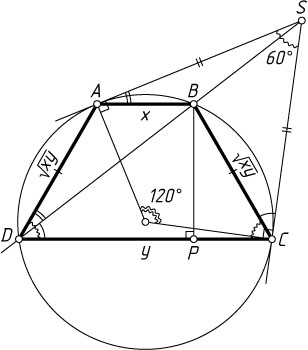
165. Из точки вне окружности проведены касательные и секущая, причём точки касания и точки пересечения секущей с окружностью являются вершинами некоторой трапеции. Найдите отношение оснований трапеции, если известно, что угол между касательными равен 60^{\circ}
.
Ответ. \frac{3-\sqrt{5}}{2}
.
Указание. Пусть S
— данная точка, SBD
— секущая, A
и C
— точки касания и AB\parallel CD
. Тогда треугольник SBC
подобен треугольнику SCD
, а треугольник SBA
— треугольнику SAD
.
Решение. Пусть S
— данная точка, SBD
— секущая, SA
и SC
— касательные, AB\parallel DC
. Обозначим AB=x
, CD=y
.
Из подобия треугольников SBC
и SCD
(по двум углам) следует, что \frac{BC}{DC}=\frac{SB}{CS}
, а из подобия треугольников SBA
и SAD
— \frac{AB}{AD}=\frac{SB}{AS}
.
Поскольку CS=AS
, то \frac{AB}{AD}=\frac{BC}{DC}
, или AB\cdot DC=xy=BC^{2}
. Отсюда находим, что BC=\sqrt{xy}
. Кроме того,
\angle BCD=\angle ADC=60^{\circ}.
Если P
— проекция точки B
на основание CD
трапеции ABCD
, то PC=\frac{y-x}{2}
. В треугольнике BPC
имеем:
PC=\frac{1}{2}BC,~\mbox{или}~\frac{y-x}{2}=\frac{\sqrt{xy}}{2},~\mbox{или}~\frac{x}{y}+\sqrt{\frac{x}{y}}-1=0.
Из этого уравнения находим, что
\frac{x}{y}=\frac{3-\sqrt{5}}{2}.
Источник: Вступительный экзамен на механико-математический и экономический факультеты НГУ. — 1974
Источник: Журнал «Квант». — 1975, № 4, с. 48, задача 2, вариант 1
