166. Диагонали выпуклого четырёхугольника взаимно перпендикулярны. Докажите, что четыре проекции точки пересечения диагоналей на стороны четырёхугольника лежат на одной окружности.
Указание. Точка пересечения диагоналей, её проекции на соседние стороны и общая точка этих сторон лежат на одной окружности.
Решение. Пусть O
— точка пересечения диагоналей AC
и BD
четырёхугольника ABCD
; M
, N
, P
, Q
— проекции точки O
на AB
, BC
, CD
и AD
. Тогда
\angle QMO+\angle QPO=\angle QAO+\angle QDO=90^{\circ}
(так как точки M
и Q
лежат на окружности с диаметром AO
, а точки P
и Q
— на окружности с диаметром OD
). Аналогично \angle OMN+\angle OPN=90^{\circ}
. Поэтому
\angle QPN+\angle QMN=180^{\circ}.
Следовательно, четырёхугольник MNPQ
— вписанный.
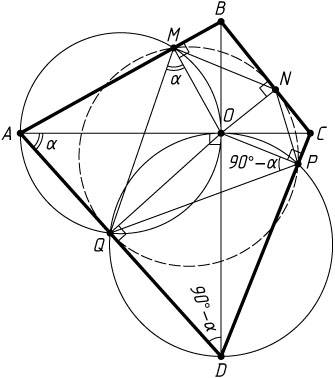
Примечание. Верно и обратное: если в четырёхугольнике ABCD
основания перпендикуляров, опущенных из точки пересечения диагоналей на стороны, являются вершинами вписанного четырёхугольника, то диагонали четырёхугольника ABCD
перпендикулярны. Это доказывается точно так же.
Автор: Кушнир И. А.
Автор: Михайловский В. И.
Источник: Журнал «Квант». — 1972, № 9, с. 37, M163; 1973, № 5, с. 33, M163; 1979, № 10, с. 61, задача 9(а)
Источник: Всесоюзная олимпиада по математике. — 1978-1979, XIII
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.20, с. 153
