168. Дан правильный треугольник ABC
. Некоторая прямая, параллельная прямой AC
, пересекает прямые AB
и BC
в точках M
и P
соответственно. Точка D
— центр правильного треугольника PMB
, точка E
— середина отрезка AP
. Найдите углы треугольника DEC
.
Ответ. 90^{\circ}
, 60^{\circ}
, 30^{\circ}
.
Указание. Пусть C_{1}
— образ точки C
при симметрии относительно точки E
. Тогда треугольник C_{1}DM
равен треугольнику CDP
. Тогда C_{1}D=CD
.
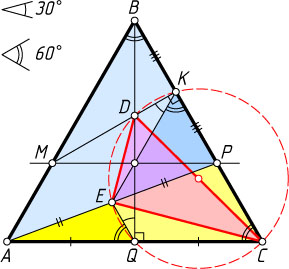
Решение. Первый способ. Пусть K
— проекция точки D
на BC
, а Q
— проекция точки B
на AC
. Точки K
, D
, Q
и C
лежат на окружности с диаметром CD
. Поскольку
\angle EQD=\angle AQD-\angle AQE=90^{\circ}-60^{\circ}=30^{\circ},
\angle DKE=\angle DKC-\angle EKC=90^{\circ}-\angle ABC=90^{\circ}-60^{\circ}=30^{\circ},
то отрезок DE
виден из точек Q
и K
под одним и тем же углом. Следовательно, точки K
, D
, E
, Q
лежат на той же окружности. Поэтому
\angle DEC=90^{\circ},~\angle DCE=\angle DQE=30^{\circ}.
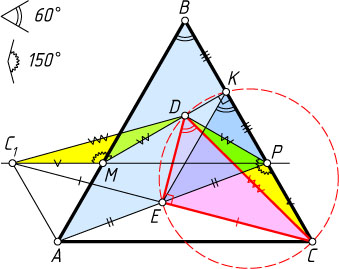
Второй способ. Пусть C_{1}
— образ точки C
при симметрии относительно точки E
. Треугольник C_{1}DM
равен треугольнику CDP
, так как
C_{1}M=C_{1}P-MP=AC-MP=BC-BP=PC,
MD=DP,~\angle C_{1}MD=\angle CPD=150^{\circ}.
Поэтому C_{1}D=CD
. Следовательно, медиана DE
равнобедренного треугольника C_{1}DC
является его высотой. Пусть K
— середина отрезка BP
. Тогда EK
— средняя линия треугольника APB
, а так как точки E
и K
лежат на окружности с диаметром CD
, то
\angle EDC=\angle EKC=60^{\circ},~\angle DEC=90^{\circ},~\angle DCE=30^{\circ}.
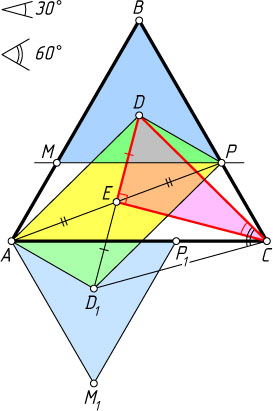
Третий способ. Повернём треугольник BMP
на 60^{\circ}
относительно точки C
так, чтобы точка B
перешла в A
. Тогда точка P
перейдёт в точку P_{1}
отрезка AC
, точка M
— в точку M_{1}
, лежащую вне треугольника ABC
, точка D
— в точку D_{1}
, центр треугольника AM_{1}P_{1}
.
Четырёхугольник DPD_{1}A
— параллелограмм, DD_{1}
— его диагональ. Поэтому D_{1}D
проходит через точку E
и D_{1}E=DE
.
Поскольку CE
— медиана равнобедренного треугольника DCD_{1}
(CD=CD_{1})
, то \angle CED=90^{\circ}
, а так как \angle DCD_{1}=60^{\circ}
, то \angle DCE=30^{\circ}
.
Автор: Купцов Л. П.
Источник: Всесоюзная олимпиада по математике. — 1980, XIV, 9 класс
Источник: Журнал «Квант». — 1980, № 11, с. 46, задача 7, 9 класс
Источник: Австрийско-польские математические олимпиады. — 1982
Источник: Австрийские математические олимпиады. — 1991, № 10, задача 15, с. 296
Источник: Васильев Н. Б., Егоров А. А. Задачи всесоюзных математических олимпиад. — М.: Наука, 1988. — № 298, с. 77
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 18.18, с. 375
Источник: Московская математическая регата. — 2019-2020, четвёртый тур, № 2, 10 класс


