170. Докажите, что для любого треугольника проекция диаметра описанной окружности, перпендикулярного одной стороне треугольника, на прямую, содержащую вторую сторону, равна третьей стороне.
Указание. Воспользуйтесь формулой a=2R\sin\alpha
.
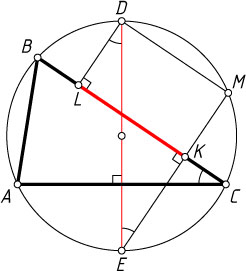
Решение. Первый способ. Пусть DE
— диаметр описанной окружности, перпендикулярный стороне AC
треугольника ABC
, R
— радиус этой окружности, LK
— проекция диаметра DE
на прямую BC
(L
— проекция точки D
, K
— точки E
). Тогда
LK=DE\sin\angle DEK=2R\sin\angle DEK=2R\sin\angle BCA=AB.
Второй способ. Продлим отрезок KE
до пересечения с окружностью в точке M
. Тогда DMKL
— прямоугольник. На хорду DM
опирается угол DEM
, равный ACB
(углы с соответственно перпендикулярными сторонами). Вписанный угол ACB
опирается на хорду AB
, следовательно, KL=DM=AB
.
Автор: Овчинников С. В.
Источник: Журнал «Квант». — 1979, № 11, с. 25, М592
Источник: Задачник «Кванта». — М592
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.166, с. 121
