173. Докажите, что в любом треугольнике ABC
середина стороны BC
лежит на отрезке, соединяющем точку пересечения высот с точкой окружности, описанной около этого треугольника, диаметрально противоположной вершине A
, и делит этот отрезок пополам.
Указание. Если AA_{1}
— диаметр описанной окружности, а H
— точка пересечения высот треугольника ABC
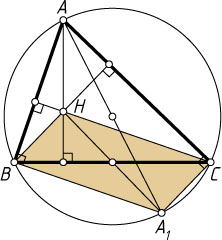
, то четырёхугольник HBA_{1}C
— параллелограмм.
Решение. Пусть AA_{1}
— диаметр описанной окружности, H
— точка пересечения высот треугольника ABC
. Тогда
A_{1}C\parallel BH,~A_{1}B\parallel CH,
поэтому четырёхугольник HBA_{1}C
— параллелограмм. Следовательно, середина его диагонали BC
лежит на диагонали HA_{1}
и делит её пополам.
Автор: Грошев Г.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 121, с. 42
Источник: Журнал «Квант». — 1980, № 1, с. 31, М601
Источник: Задачник «Кванта». — М601
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.89, с. 40
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.93, с. 40
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 458, с. 55
