177. Две окружности пересекаются в точках A
и B
. Через точку K
первой окружности проводятся прямые KA
и KB
, вторично пересекающие другую окружность в точках P
и Q
. Докажите, что хорда PQ
второй окружности перпендикулярна диаметру KM
первой окружности.
Указание. Докажите, что касательная к первой окружности, проведённая через точку K
, параллельна PQ
.
Решение. Пусть точка Q
принадлежит лучу KB
. Проведём касательную KF
к первой окружности (точки F
и Q
лежат по разные стороны от прямой AK
). Тогда KF
перпендикулярно диаметру KM
и
\angle AKF=\angle ABK=\angle APQ.
Следовательно, KF\parallel PQ
. Поэтому прямая PQ
перпендикулярна диаметру KM
.
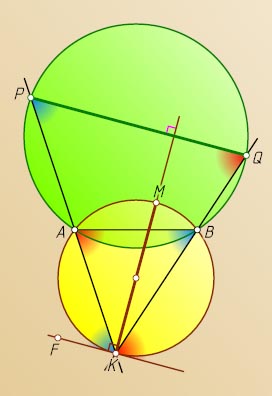
Источник: Журнал «Квант». — 1983, № 6, с. 47, М794
Источник: Задачник «Кванта». — М794
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.22, с. 33
