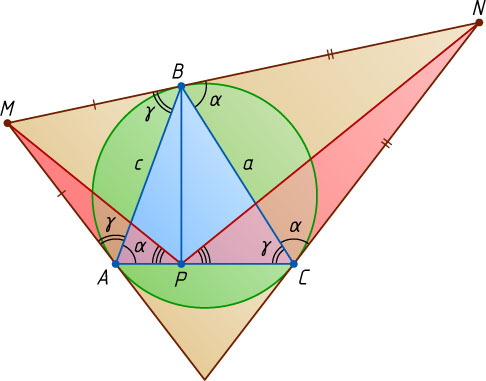
178. Около остроугольного треугольника ABC
описана окружность. Касательные к окружности, проведённые в точках A
и C
, пересекают касательную, проведённую в точке B
, соответственно в точках M
и N
. В треугольнике ABC
проведена высота BP
. Докажите, что BP
— биссектриса угла MPN
.
Указание. Докажите, что треугольники AMP
и CNP
подобны.
Решение. Пусть
AB=c,~BC=a,~\angle BAC=\alpha,~\angle BCA=\gamma.
Из теоремы об угле между касательной и хордой следует, что
\angle BAM=\angle ABM=\angle ACB=\gamma,~\angle BCN=\angle CBN=\angle BAC=\alpha.
Тогда
\angle MAP=\alpha+\gamma=\angle NCP,~AP=c\cos\alpha,~CP=a\cos\gamma,
NC=\frac{a}{2\cos\alpha},~MA=\frac{c}{2\cos\gamma}.
Поэтому
\frac{AP}{CP}=\frac{MA}{NC}=\frac{\cos\alpha}{\cos\gamma}.
Значит, треугольники AMP
и CNP
подобны. Следовательно,
\angle APM=\angle CPN,~\angle MPB=\angle NPB.
Автор: Чиник Б. И.
Источник: Всесоюзная олимпиада по математике. — 1988, XXII
Источник: Журнал «Квант». — 1988, № 11-12, с. 39, М1111
Источник: Задачник «Кванта». — М1111
Источник: Кушнир И. А. Геометрия. Поиск и вдохновение. — М.: МЦНМО, 2013. — с. 49
