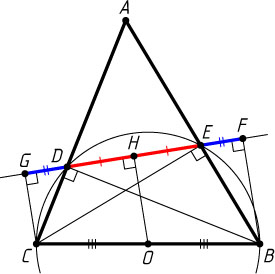
179. В остроугольном треугольнике ABC
проведены высоты BD
и CE
. Из вершин B
и C
на прямую ED
опущены перпендикуляры BF
и CG
. Докажите, что EF=DG
.
Указание. Опустите перпендикуляр из середины стороны BC
на прямую DE
.
Решение. Поскольку из точек D
и E
отрезок BC
виден под прямым углом, то точки B
, C
, D
и E
лежат на окружности с центром в середине O
стороны BC
.
Пусть H
— основание перпендикуляра, опущенного из точки O
на DE
. Тогда DH=HE
(диаметр, перпендикулярный хорде, делит её пополам) и GH=HF
, так как OH
— средняя линия трапеции BFGH
. Следовательно, EF=DG
.
Автор: Струков С.
Источник: Всесоюзная олимпиада по математике. — 1988, XXII
Источник: Журнал «Квант». — 1988, № 11-12, с. 76, задача 1, 10 класс
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 68, с. 144
Источник: Всероссийская олимпиада школьников. — 2016-2017, XLIII, окружной этап, 9 класс
Источник: Агаханов Н. Х., Подлипский О. К. Математика. Районные олимпиады. — М.: Просвещение, 2010. — 2003, № 289, с. 77, 9 класс, задача 4
