180. В трапеции ABCD
с основаниями BC
и AD
на сторонах AB
и CD
выбраны точки K
и M
. Докажите, что если \angle BAM=\angle CDK
, то \angle BMA=\angle CKD
.
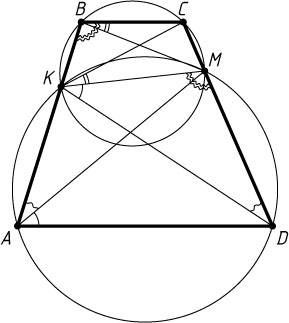
Указание. Точки A
, K
, M
, D
принадлежат одной окружности, и точки K
, B
, C
, M
также принадлежат одной окружности.
Решение. Точки A
, K
, M
, D
лежат на одной окружности. Поэтому
\angle KMD=180^{\circ}-\angle KAD=\angle KBC,~\angle KMC+\angle KBC=180^{\circ}.
Тогда точки K
, B
, C
, M
также лежат на одной окружности. Следовательно,
\angle CKD=\angle CKM+\angle MKD=\angle CBM+\angle MAD=
=180^{\circ}-(\angle BAM+\angle MBA)=\angle BMA.
