184. Точка D
лежит на биссектрисе угла ACB
. На луче CA
выбрали точки A_{1}
и A_{2}
, а на луче CB
— точки B_{1}
и B_{2}
, причём четыре точки A_{1}
, C
, B_{1}
, D
лежат на одной окружности и четыре точки A_{2}
, C
, B_{2}
, D
также лежат на одной окружности. Докажите, что A_{1}A_{2}=B_{1}B_{2}
.
Указание. Докажите, что треугольник DA_{1}A_{2}
равен треугольнику DB_{1}B_{2}
.
Решение. Пусть A_{1}
находится между точками C
и A_{2}
, а B_{2}
— между C
и B_{1}
. Треугольники DA_{1}A_{2}
и DB_{1}B_{2}
равны, так как
DA_{1}=DB_{1},~DA_{2}=DB_{2},
\angle A_{1}DA_{2}=\angle B_{2}DA_{2}-\angle A_{1}DB_{2}=180^{\circ}-\angle C-\angle A_{1}DB_{2}=
=\angle B_{1}DA_{1}-\angle A_{1}DB_{2}=\angle B_{1}DB_{2}.
Следовательно,
A_{1}A_{2}=B_{1}B_{2}.
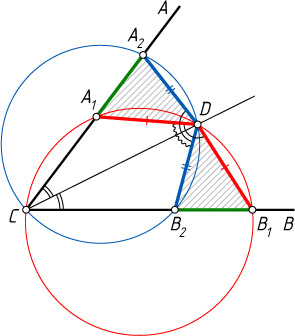
Источник: Журнал «Квант». — 1974, № 1, с. 73, задача 6
