186. На сторонах угла ABC
, равного 120^{\circ}
, отложены отрезки AB=BC=4
. Через точки A
, B
, C
проведена окружность. Найдите её радиус.
Ответ. 4.
Указание. Центр окружности — точка пересечения серединных перпендикуляров к сторонам треугольника ABC
.
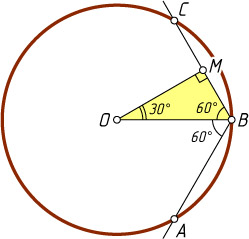
Решение. Пусть M
— середина отрезка BC
, O
— центр окружности. Тогда OM\perp BC
, BO
— биссектриса угла ABC
, \angle BOM=30^{\circ}
, BM=2
. Поэтому R=BO=2BM=4
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 1, с. 28
