187. Найдите геометрическое место центров окружностей, имеющих данный радиус и проходящих через данную точку.
Ответ. Окружность того же радиуса с центром в данной точке.
Указание. Вспомните определение окружности.
Решение. Пусть R
— данный радиус. Тогда центры всех окружностей радиуса R
, проходящих через данную точку O
, удалены от этой точки на расстояние, равное R
. Значит, они лежат на окружности радиуса R
с центром O
.
Обратно, каждая точка этой окружности удалена от точки O
на расстояние, равное R
.
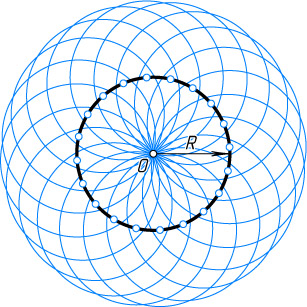
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 2, с. 28
