190. Из точки, данной на окружности, проведены диаметр и хорда, равная радиусу. Найдите угол между ними.
Ответ. 60^{\circ}
.
Указание. Любая отличная от диаметра хорда окружности есть основание равнобедренного треугольника с вершиной в центре окружности.
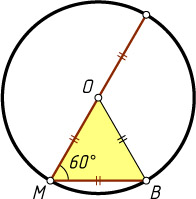
Решение. Пусть M
— точка на окружности, O
— центр окружности, BM
— хорда. Тогда BM=OM=OB
. Следовательно, треугольник BMO
— равносторонний.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 8, с. 29
