192. В круге даны две взаимно перпендикулярные хорды. Каждая из них делится другой хордой на два отрезка, равных 3 и 7. Найдите расстояние от центра окружности до каждой хорды.
Ответ. 2.
Указание. Диаметр, перпендикулярный хорде, делит её пополам.
Решение. Пусть N
и M
— основания перпендикуляров, опущенных из центра O
окружности на данные хорды, A
— точка пересечения хорд. Тогда N
и M
— середины хорд, а четырёхугольник OMAN
— квадрат. Следовательно,
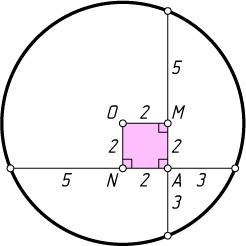
ON=AM=5-3=2,~OM=2.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 10, с. 29
