194. В круге радиуса R
даны два взаимно перпендикулярных диаметра. Произвольная точка окружности спроектирована на эти диаметры. Найдите расстояние между проекциями точки.
Ответ. R
.
Указание. Диагонали прямоугольника равны.
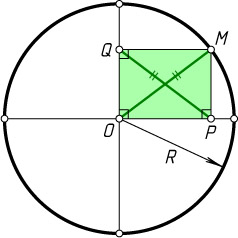
Решение. Пусть M
— данная точка, P
и Q
— её проекции на данные диаметры, O
— центр круга. Тогда MPOQ
— прямоугольник. Поскольку диагонали прямоугольника равны, то PQ=OM=R
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 12, с. 29
