195. Хорда пересекает диаметр под углом 30^{\circ}
и делит его на два отрезка, равные 2 и 6. Найдите расстояние от центра окружности до этой хорды.
Ответ. 1.
Указание. Катет, лежащий против угла в 30^{\circ}
, равен половине гипотенузы.
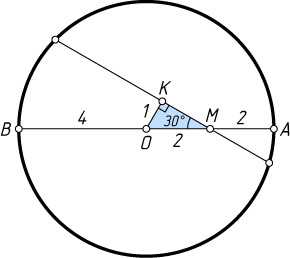
Решение. Пусть O
— центр окружности, M
— точка пересечения данной хорды и диаметра AB
(AM=2
, MB=6
), K
— основание перпендикуляра, опущенного из центра O
на данную хорду. Тогда
MO=AO-AM=2,~OK=\frac{1}{2}MO=1.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 13, с. 29
