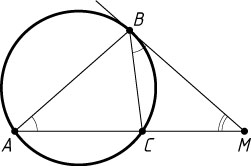
196. Около треугольника ABC
описана окружность. Касательная к окружности, проходящая через точку B
, пересекает прямую AC
в точке M
. Найдите отношение \frac{AM}{MC}
, если \frac{AB}{BC}=k
.
Ответ. k^{2}
.
Решение. Из теоремы об угле между касательной и хордой следует, что
\angle CBM=\angle BAC=\angle BAM,
поэтому треугольник ABM
подобен треугольнику BCM
, значит, \frac{BM}{MC}=\frac{AB}{BC}
и \frac{AM}{MB}=\frac{AB}{BC}
. Перемножив эти равенства, получим, что
\frac{BM}{MC}\cdot\frac{AM}{MB}=\left(\frac{AB}{BC}\right)^{2}=k^{2},
или \frac{AM}{MC}=k^{2}
.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 234, с. 27
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 2.4, с. 23
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 12.39.1, с. 128
