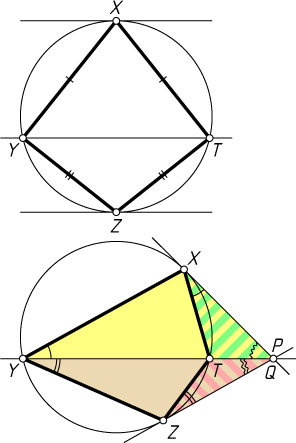
197. Докажите, что если четырёхугольник XYZT
вписан в окружность и \frac{XY}{XT}=\frac{ZY}{ZT}
, то касательные к окружности, проведённые в точках X
и Z
, либо параллельны, либо пересекаются на прямой YT
.
Решение. Если одна из касательных, например, в точке X
, параллельна прямой YT
, то XY=XT
. Тогда ZY=ZT
. Следовательно, касательная в точке Z
также параллельна YT
.
Пусть прямая YT
пересекает касательную, проведённую к окружности в точке X
, в точке P
. Из теоремы об угле между касательной и хордой следует, что \angle PXT=\angle TYX=\angle PYX
, значит, треугольники PXY
и PTX
подобны по двум углам. Поэтому \frac{YP}{XP}=\frac{XY}{XT}
и \frac{XP}{TP}=\frac{XY}{XT}
. Перемножив эти равенства, получим, что \frac{YP}{TP}=\left(\frac{XY}{XT}\right)^{2}
.
Пусть прямая YT
пересекает касательную, проведённую к окружности в точке Z
, в точке Q
. Аналогично докажем, что \frac{YQ}{TQ}=\left(\frac{XY}{XT}\right)^{2}
, поэтому \frac{YP}{TP}=\frac{YQ}{TQ}
. Значит, точки P
и Q
совпадают. Отсюда следует утверждение задачи.