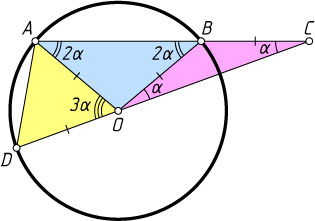
198. Дана окружность с центром O
. На продолжении хорды AB
за точку B
отложен отрезок BC
, равный радиусу. Через точки C
и O
проведена секущая CD
(D
— точка пересечения с окружностью, лежащая вне отрезка CO
). Докажите, что \angle AOD=3\angle ACD
.
Указание. Треугольники OBC
и AOB
— равнобедренные, ABO
— внешний угол треугольника OBC
, \angle AOD
— внешний угол треугольника AOC
.
Решение. Обозначим \angle ACD=\alpha
. Так как BC=OB
, то \angle BOC=\alpha
. Поэтому \angle ABO=2\alpha
(как внешний угол треугольника OBC
).
Из равнобедренного треугольника BOA
находим, что
\angle BAO=\angle ABO=2\alpha.
Тогда
\angle AOD=\angle CAO+\angle ACD=3\alpha,
так как \angle AOD
— внешний угол треугольника OAC
.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 15, с. 31
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 16, с. 29
