199. Докажите, что середины всех хорд данной длины, проведённых в данной окружности, лежат на некоторой окружности.
Указание. Середина каждой такой хорды — это основание перпендикуляра, опущенного из центра окружности на эту хорду.
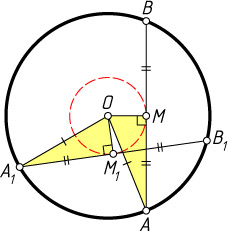
Решение. Рассмотрим две отличные от диаметра равные хорды AB
и A_{1}B_{1}
окружности с центром O
. Пусть M
и M_{1}
— основания перпендикуляров, опущенных из точки O
на эти хорды. Тогда из равенства треугольников OM_{1}A_{1}
и OMA
следует, что OM=OM_{1}
. Но M
и M_{1}
— середины данных хорд.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 17(2), с. 29
