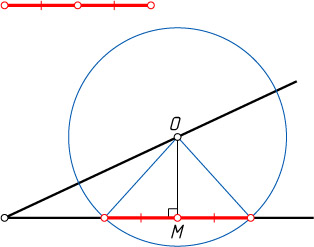
201. Постройте окружность с центром в данной точке на стороне данного острого угла, которая на другой стороне угла отсекала бы хорду данной длины.
Указание. Диаметр, перпендикулярный хорде, делит её пополам.
Решение. Опустим перпендикуляр OM
из данной точки O
на вторую сторону угла и отложим на этой стороне от его основания в разные стороны отрезки, равные половине данной хорды. Радиус искомой окружности равен расстоянию от центра до концов полученного отрезка.
Если половина данной хорды не больше расстояния от точки M
до вершины данного угла, то задача имеет единственное решение. В противном случае задача не имеет решений.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 19, с. 30
