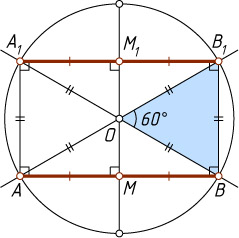
202. В данном круге проведены две равные параллельные хорды, расстояние между которыми равно радиусу данного круга. Найдите острый угол между прямыми, соединяющими концы хорд.
Ответ. 60^{\circ}
.
Указание. Докажите, что указанные прямые пересекаются в центре окружности.
Решение. Пусть AB
и A_{1}B_{1}
— равные параллельные хорды. Проведём через центр O
окружности диаметр, перпендикулярный хорде AB
. Тогда он перпендикулярен и хорде A_{1}B_{1}
и проходит через середины M
и M_{1}
данных хорд.
Четырёхугольник ABB_{1}A_{1}
— параллелограмм, а значит, — прямоугольник, диагонали которого пересекаются в точке O
. Если R
— радиус окружности, то BB_{1}=MM_{1}=R
. Тогда треугольник BOB_{1}
— равносторонний. Следовательно, \angle BOB_{1}=60^{\circ}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 20, с. 30
