204. Дан сектор, равный четверти круга радиуса R
. Найдите длину касательной, проведённой в середине его дуги до пересечения с продолжением крайних радиусов сектора.
Ответ. 2R
.
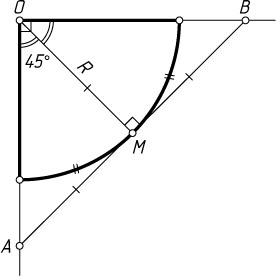
Указание. Пусть O
— центр окружности, M
— точка касания. Докажите, что луч OM
образует углы в 45^{\circ}
с радиусами, ограничивающими данный сектор.
Решение. Пусть O
— центр окружности, лучи OA
и OB
образуют прямой угол и пересекаются с данной касательной в точках A
и B
, M
— точка касания. Тогда
\angle MOB=\angle MOA=\frac{1}{2}\angle AOB=45^{\circ}.
Поэтому
MB=MO=R,~MA=MO=R.
Следовательно, AB=2R
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 22, с. 30
