207. Радиусы двух окружностей равны 2 и 4. Их общие внутренние касательные взаимно перпендикулярны. Найдите длину каждой из них.
Ответ. 6.
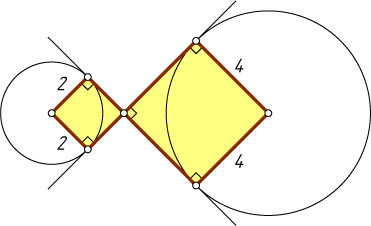
Указание. Для каждой из данных окружностей четырёхугольник, образованный указанными касательными и радиусами, проведёнными в точки касания, — квадрат.
Решение. Для каждой из данных окружностей четырёхугольник, образованный касательными и радиусами, проведёнными в точки касания, — квадрат. Поэтому длина искомой касательной равна сумме радиусов, т. е. сторон квадратов.

Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 27, с. 31