208. Даны две окружности. Их общие внутренние касательные взаимно перпендикулярны. Хорды, соединяющие точки касания, равны 3 и 5. Найдите расстояние между центрами окружностей.
Ответ. 8.
Указание. Для каждой из окружностей четырёхугольник, образованный касательными и радиусами, проведёнными в точки касания, — квадрат.
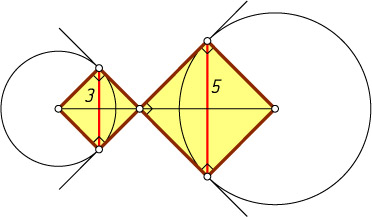
Решение. Для каждой из окружностей четырёхугольник, образованный касательными и радиусами, проведёнными в точки касания, — квадрат. Отрезок, соединяющий точку пересечения касательных с центром окружности, — диагональ квадрата. Сумма этих отрезков и есть расстояние между центрами.

Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 28, с. 31