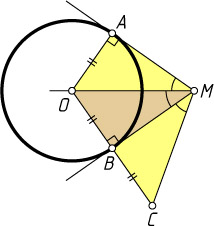
216. Две прямые проходят через точку M
и касаются окружности в точках A
и B
. Проведя радиус OB
, продолжают его за точку B
на расстояние BC=OB
. Докажите, что \angle AMC=3\angle BMC
.
Указание. MB
— биссектриса угла OMC
, MO
— биссектриса угла AMB
.
Решение. В треугольнике OMC
высота MB
является медианой. Поэтому треугольник OMC
— равнобедренный, и MB
— биссектриса угла OMC
. Но MO
— биссектриса угла AMB
. Следовательно,
\angle AMB=2\angle OMB=2\angle BMC,~\angle AMC=3\angle BMC.
