218. Пусть r
— радиус окружности, касающейся гипотенузы и продолжений катетов прямоугольного треугольника со сторонами a
, b
, c
. Докажите, что r=\frac{a+b+c}{2}
.
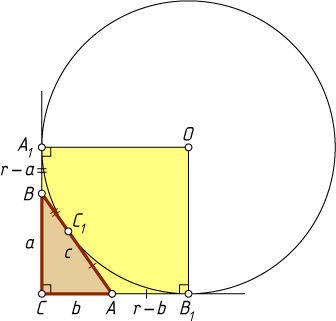
Указание. Четырёхугольник, образованный прямыми, содержащими катеты, и радиусами, проведёнными в точки касания с продолжениями катетов, — квадрат.
Решение. Обозначим вершины треугольника, противолежащие сторонам a
, b
, c
, через A
, B
, C
(C
— вершина прямого угла), а точки касания — через A_{1}
, B_{1}
, C_{1}
соответственно. Если O
— центр данной окружности, то OA_{1}CB_{1}
— квадрат со стороной, равной r
. Поэтому
CA_{1}=r,~BC_{1}=BA_{1}=r-a,~AC_{1}=AB_{1}=r-b,
c=AB=AC_{1}+C_{1}B=2r-a-b.
Следовательно, r=\frac{a+b+c}{2}
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.15 (фрагмент), с. 106
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4(б), с. 56, № 5.18(б), с. 103
