219. В треугольник ABC
вписана окружность. Пусть x
— расстояние от вершины A
до точки касания окружности со стороной AB
, BC=a
. Докажите, что x=p-a
, где p
— полупериметр треугольника.
Указание. Используя равенство касательных, проведённых к окружности из одной точки, выразите сторону, равную a
, через остальные стороны треугольника и указанный отрезок x
.
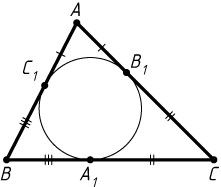
Решение. Обозначим точки касания вписанной окружности со сторонами AB
, BC
и AC
через C_{1}
, A_{1}
и B_{1}
соответственно. Пусть AC=b
и AB=c
. Тогда
BA_{1}=BC_{1}=AB-AC_{1}=c-x,~CA_{1}=CB_{1}=AC-AB_{1}=b-x,
BC=BA_{1}+CA_{1}=c-x+b-x=b+c-2x.
Следовательно,
x=\frac{b+c-a}{2}=\frac{b+c+a}{2}-a=p-a.
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 228, с. 23
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 18, с. 8
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 18, с. 6
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — № 16, с. 110
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 81
