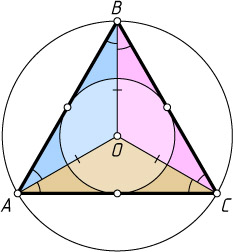
220. Центр окружности, описанной около треугольника, совпадает с центром вписанной окружности. Найдите углы треугольника.
Ответ. 60^{\circ}
, 60^{\circ}
, 60^{\circ}
.
Указание. Пусть O
— общий центр вписанной и описанной окружностей треугольника ABC
. Тогда треугольники AOB
, AOC
, BOC
— равнобедренные, а CO
, AO
и BO
— биссектрисы углов C
, A
и B
.
Решение. Пусть O
— общий центр вписанной и описанной окружностей треугольника ABC
. Треугольник AOC
— равнобедренный. Поэтому \angle OAC=\angle OCA
. Поскольку AO
и CO
— биссектрисы углов BAC
и BCA
, то \angle BAC=\angle BCA
. Аналогично \angle BAC=\angle ABC
.
