221. Хорда стягивает дугу в 90^{\circ}
и равна 16. Найдите её расстояние от центра.
Ответ. 8.
Указание. Основание перпендикуляра, опущенного из центра окружности на указанную хорду, делит её пополам.
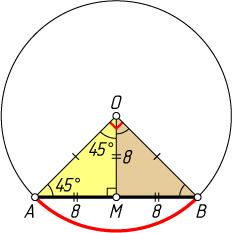
Решение. Пусть M
— основание перпендикуляра, опущенного из центра O
окружности на хорду AB
. Тогда M
— середина AB
, и треугольник OMA
— равнобедренный. Следовательно, OM=MA=8
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 5, с. 35
