222. Найдите геометрическое место центров окружностей данного радиуса R
, касающихся данной окружности радиуса r
(R\ne r
).
Ответ. Концентрические окружности, центры которых совпадают с центром данной окружности, а радиусы равны |R-r|
и R+r
.
Указание. Линия центров касающихся окружностей проходит через их точку касания.
Решение. Поскольку линия центров двух касающихся окружностей проходит через их точку касания, то искомое геометрическое место точек представляет собой две окружности, концентрические данной. Радиусы этих окружностей равны сумме и разности данных радиусов.
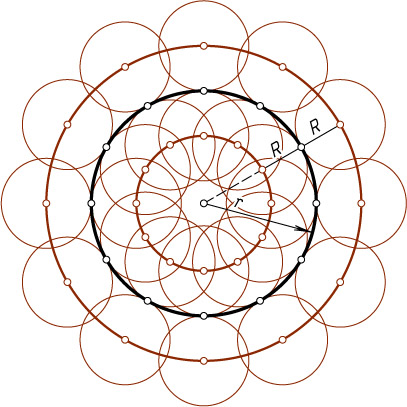
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 57, с. 76
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 54(1), с. 34
