224. С помощью циркуля и линейки постройте окружность данного радиуса, которая касалась бы данной прямой и данной окружности.
Указание. Расстояние между центрами окружностей, касающихся внешним (внутренним) образом, равно сумме (разности) их радиусов.
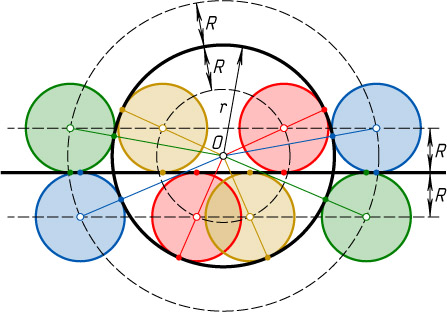
Решение. Пусть O
— центр данной окружности, r
— её радиус, R
— данный радиус. Центр искомой окружности находится на пересечении прямой, параллельной данной, проведённой на расстоянии R
от данной, и окружности с центром O
и радиусом R+r
или |R-r|
.
Задача может иметь до восьми решений.
Источник: Московская математическая олимпиада. — 1940, VI, 1-й тур, 7-8 классы
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 4, с. 24
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 54(2), с. 34
Источник: Петерсен Ю. Методы и теории для решения геометрических задач на построение, приложенные более чем к 400 задачам. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — № 8, с. 12
