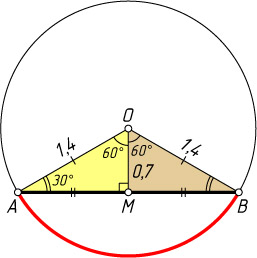
225. В окружности, радиус которой 1,4, определите расстояние от центра до хорды, если она отсекает дугу в 120^{\circ}
.
Ответ. 0,7.
Указание. Катет, лежащий против угла в 30^{\circ}
, равен половине гипотенузы.
Решение. Пусть M
— основание перпендикуляра, опущенного из центра O
на хорду AB
. Тогда OM
— катет прямоугольного треугольника OMA
, лежащий против угла в 30^{\circ}
. Следовательно,
OM=\frac{1}{2}OA=0{,}7.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 6, с. 35
