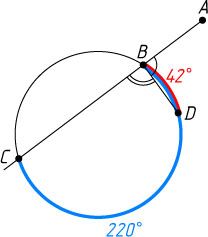
228. ABC
— секущая, A
— внешняя точка окружности, угловая величина дуги BD
равна 42^{\circ}
, а угловая величина дуги BDC
равна 220^{\circ}
. Найдите угол ABD
.
Ответ. 91^{\circ}
.
Указание. Вписанный угол равен половине угловой величины дуги, на которую он опирается.
Решение. Угол ABD
— смежный для угла DBC
, который измеряется половиной дуги DC
, не содержащей точки B
, т. е.
\angle DBC=\frac{1}{2}(220^{\circ}-42^{\circ})=89^{\circ}.
Следовательно, \angle ABD=91^{\circ}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 11, с. 35
