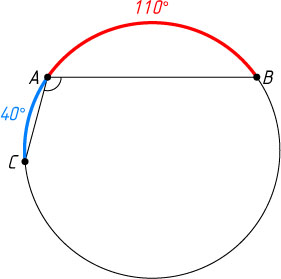
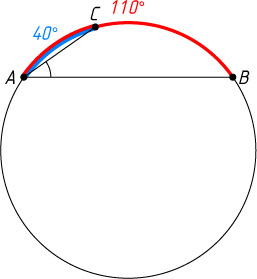
230. AB
и AC
— хорды окружности; \cup AB=110^{\circ}
, \cup AC=40^{\circ}
. Найдите угол BAC
.
Ответ. 105^{\circ}
, 35^{\circ}
.
Указание. Рассмотрите два возможных расположения точек A
, B
и C
на окружности.
Решение. В одном из возможных случаев дуга BC
, не содержащая точку A
, равна 360^{\circ}-(110^{\circ}+40^{\circ})=210^{\circ}
, а в другом — \cup BC=110^{\circ}-40^{\circ}=70^{\circ}
. Следовательно, искомый угол равен либо 105^{\circ}
, либо 35^{\circ}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 16, с. 35

