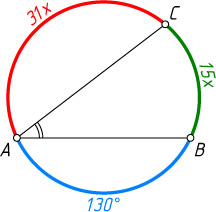
231. Хорда AB
делит окружность на две дуги, из которых меньшая равна 130^{\circ}
, а большая делится хордой AC
в отношении 31:15
, считая от точки A
. Найдите угол BAC
.
Ответ. 37^{\circ}30'
.
Указание. Вписанный угол измеряется половиной угловой величины соответствующей дуги.
Решение. Угловая величина большей дуги равна 360^{\circ}-130^{\circ}=230^{\circ}
. Угол BAC
опирается на дугу BC
, угловая величина которой равна \frac{15}{46}\cdot230^{\circ}=75^{\circ}
. Следовательно,
\angle BAC=\frac{1}{2}\cup BC=37^{\circ}30'.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 17, с. 35
