232. Окружность разделена в отношении 7:11:6
, и точки деления соединены между собой. Найдите углы полученного треугольника.
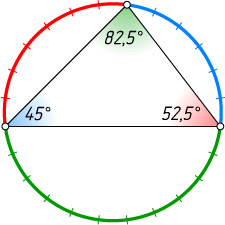
Ответ. 52{,}5^{\circ}
; 82{,}5^{\circ}
; 45^{\circ}
.
Указание. Вписанный угол измеряется половиной угловой величины соответствующей дуги.
Решение. На одну часть окружности приходится \frac{360^{\circ}}{7+11+6}=15^{\circ}
. Следовательно, угловые величины полученных дуг равны 105^{\circ}
, 165^{\circ}
и 90^{\circ}
. Углы треугольника равны половинам угловых величин этих дуг.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 19, с. 35
