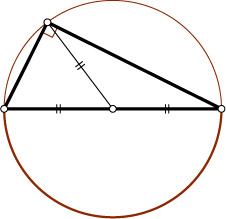
234. Если в треугольнике медиана равна половине стороны, к которой она проведена, то угол против этой стороны — прямой. Докажите это с помощью вспомогательной окружности.
Указание. Рассмотрите окружность с центром в середине указанной стороны и радиусом, равным её половине.
Решение. Поскольку медиана равна половине соответствующей стороны, то вершины треугольника расположены на окружности с центром в середине этой стороны и радиусом, равным половине этой стороны. Указанный угол опирается на дугу, угловая величина которой равна 180^{\circ}
. Следовательно, он прямой.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 21, с. 36
